Particle wavepacket animations
Animations of particle wavepackets created by Emeritus Professor John Lekner.
A0 Motion of the free-particle Gaussian wavepacket through its focal region
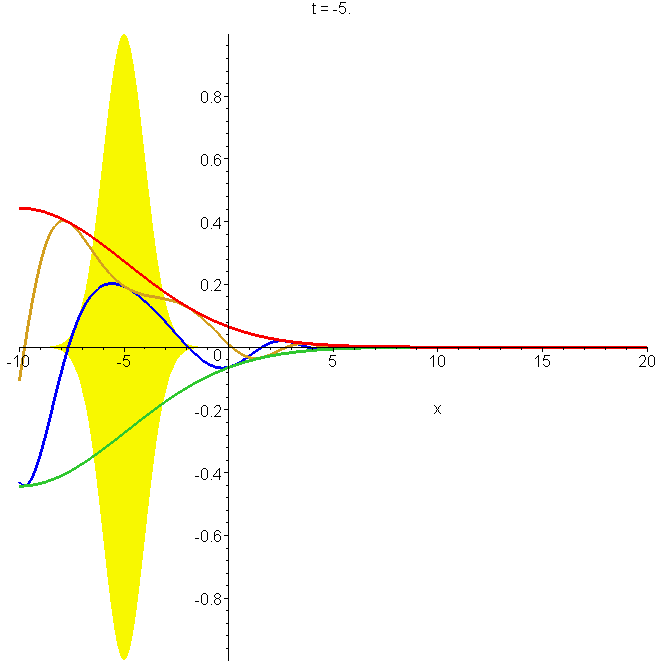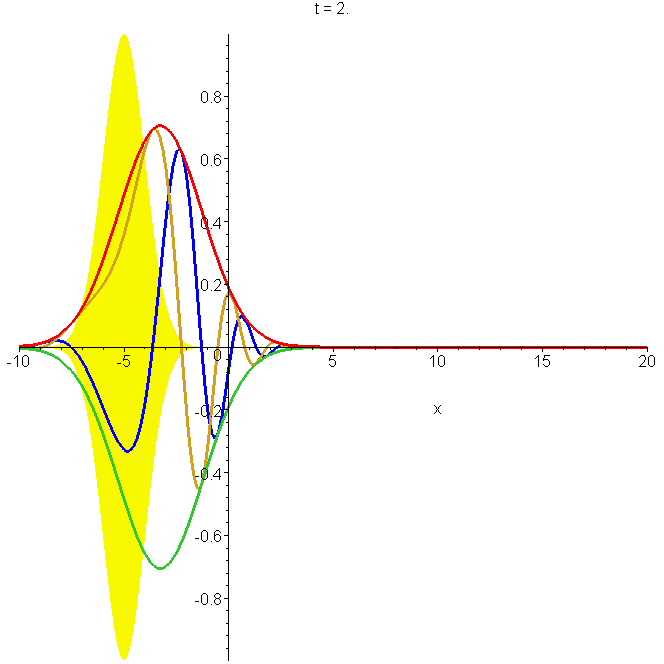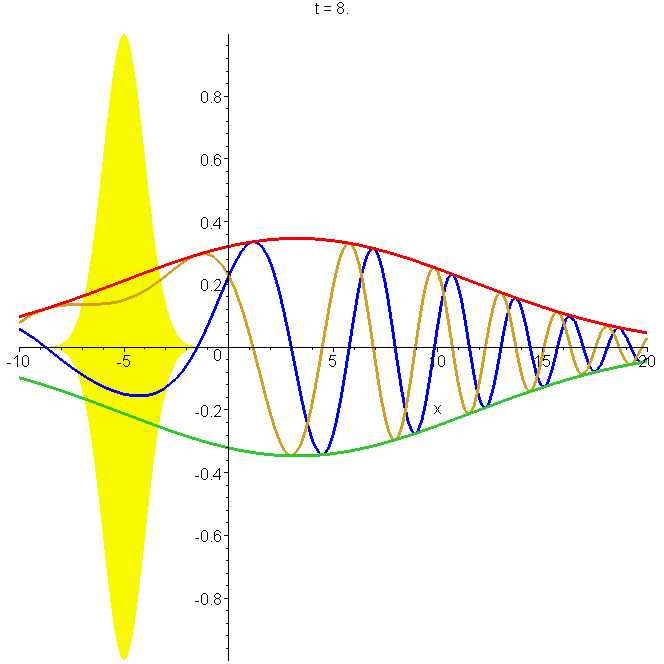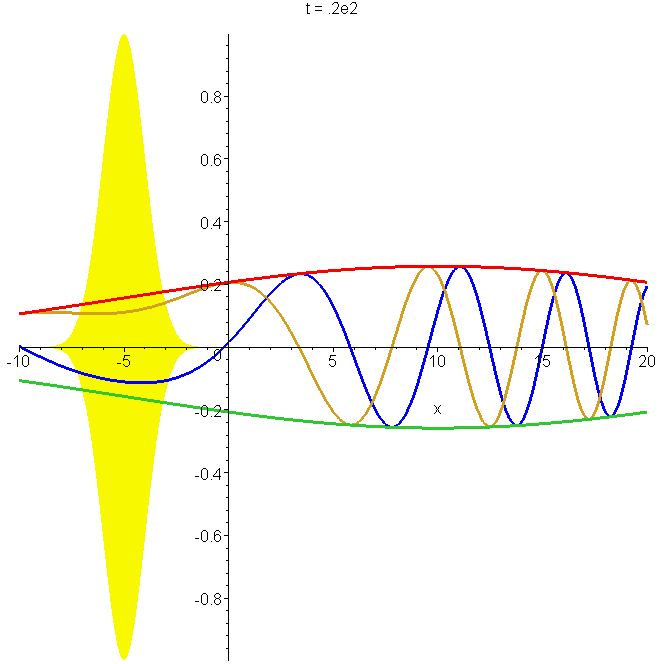
Motion of the free-particle Gaussian wavepacket \(\Phi_0(x,t)\) through its focal region. The parameters used are \(x_0=-5b\), \(k_0b=1\). The time varies from \(t=-10b/v_0\) to \(=10b/v_0\), where \(v_0=\hbar{}k_0/m\) is the group speed. The position varies from \(x=-15b\) to \(=10b\). The focal region is centred on \(x_0=-5b\) at \(t=0\); the yellow shading indicates the limits of the amplitude at focus. The real and imaginary parts of \(\Phi_0(x,t)\) are shown, as well as its modulus. Note the different wavelengths and phase speeds: see problems 2 and 3 in "Reflectionless eigenstates of the sech2 potential".
B0 Motion of the non-reflecting wavepacket \(\Phi_0(x,t)\) through the potential region
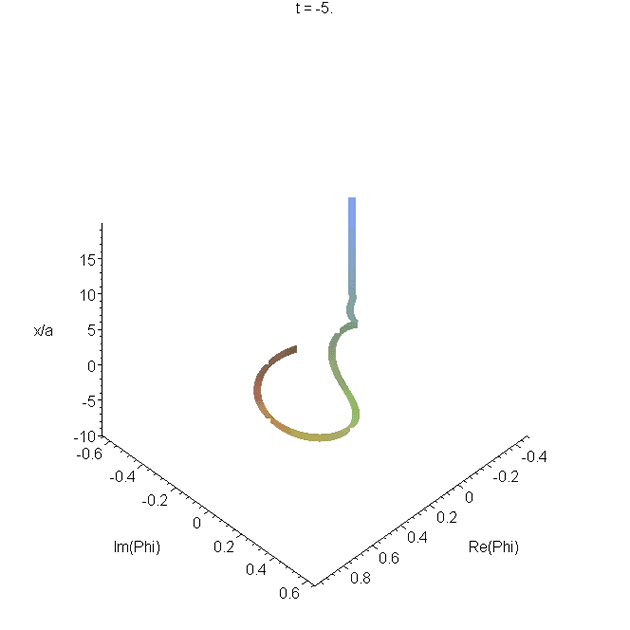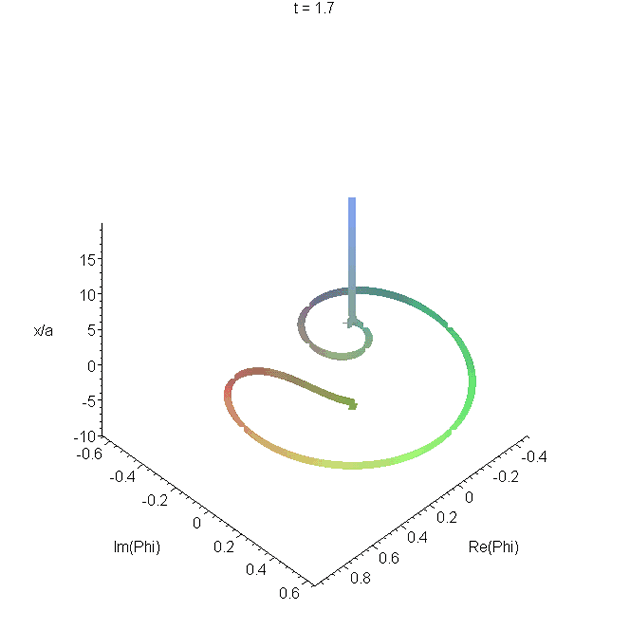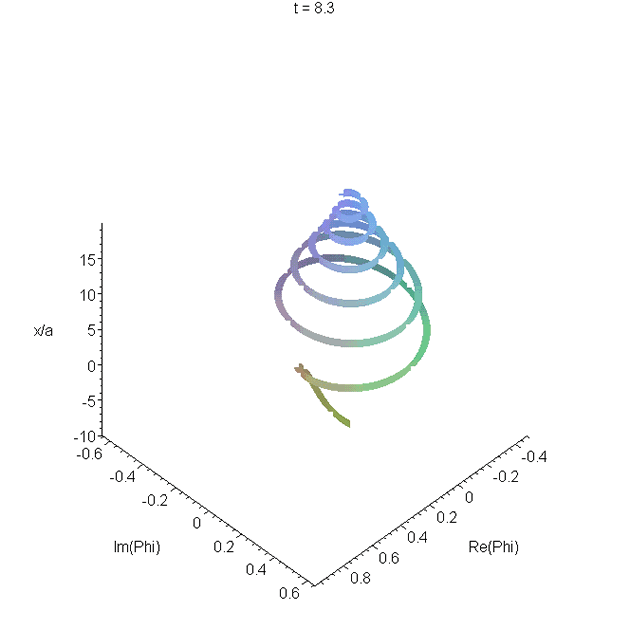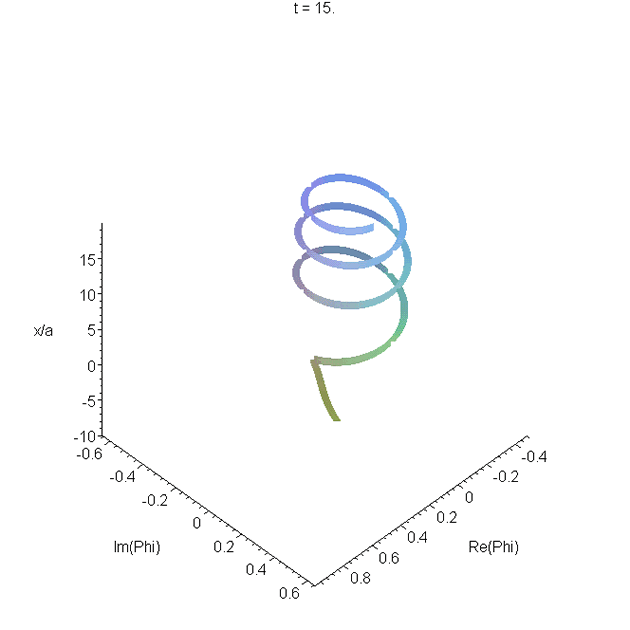
Motion of the free-particle Gaussian wavepacket \(\Phi_0(x,t)\) through its focal region. The parameters used are as in A0. The real and imaginary parts of \(\Phi_0(x,t)\) are plotted as a function of \(x\), and animated. The resulting space curve changes helicity. Most of the curve is right-handed, but there is a left-handed region in the tail. The helicity is related to increase or decrease of the phase with \(x\). See problem 4 in Reflectionless eigenstates of the sech2 potential.
A1 Motion of the non-reflecting wavepacket \(\Phi_1(x,t)\) through the potential region
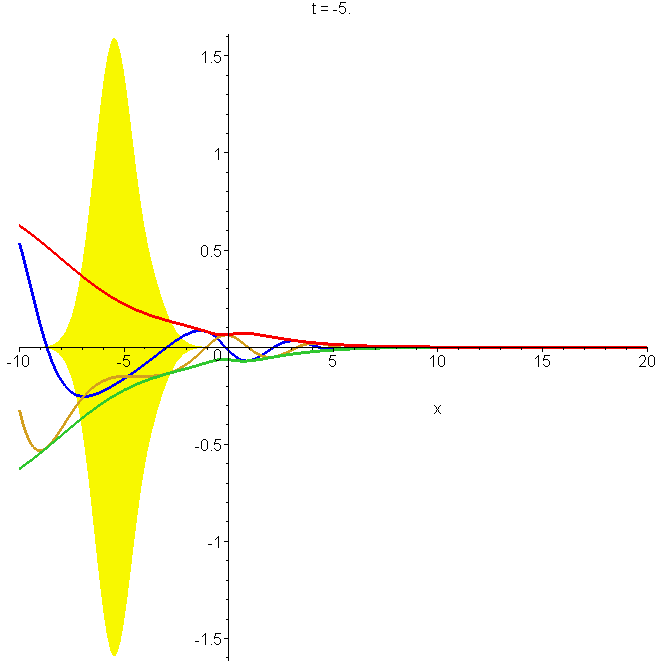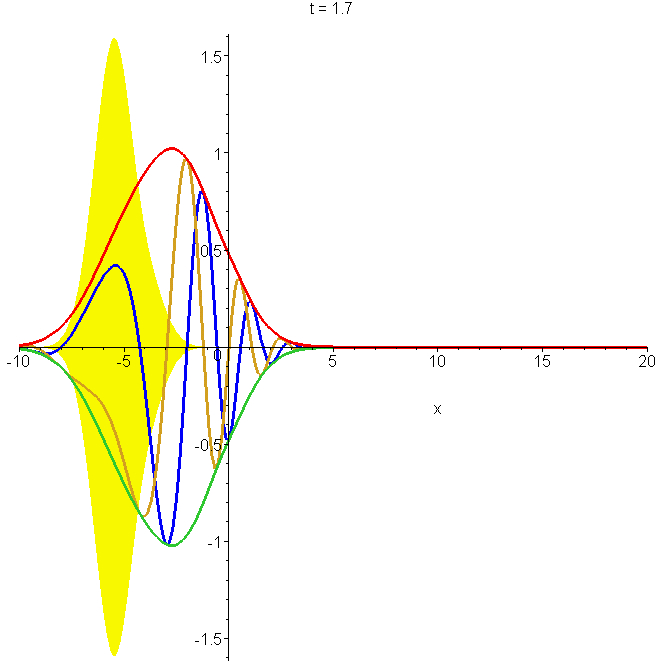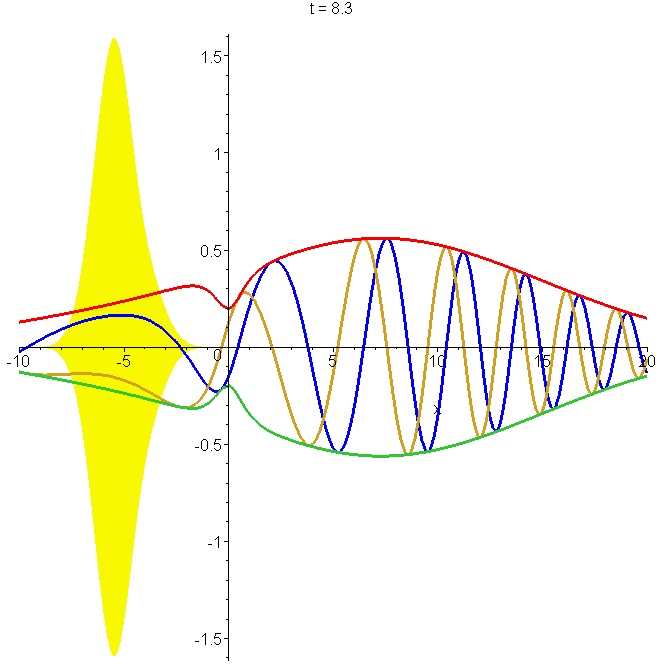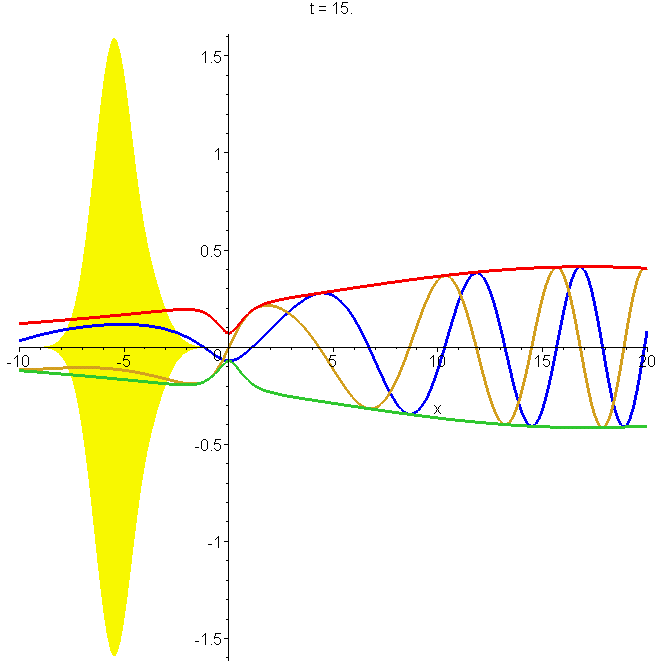
Motion of the non-reflecting wavepacket \[\Phi_1(x,t)=\left[\frac{a(x-x_0-ik_0b^2)}{b^2+i\hbar{}t/m}+\tanh{\frac{x}{a}}\right]\Phi_0(x,t)\] where \[\Phi_0(x,t)=\frac{b}{\sqrt{b^2+i\hbar{}t/m}}exp\left\{ik_0(x-x_0-\frac{1}{2}v_0t)-\frac{(x-x_0-\frac{1}{2}v_0t)^2}{2(b^2+i\hbar{}t/m)}\right\}\] through the potential \[U(x)=-\frac{\hbar^2}{ma^2}\frac{1}{\cosh^2\left(\frac{x}{a}\right)}\] The parameters are as in A0, and \(a=b\). The yellow shading indicates the limits of the amplitude at focus. Note the constriction in the probability as the packet passes over the potential well, centred on \(x=0\). See "Reflectionless eigenstates of the sech2 potential".
B1 Motion of the wavepacket \(\Phi_1(x,t)\) through the potential region
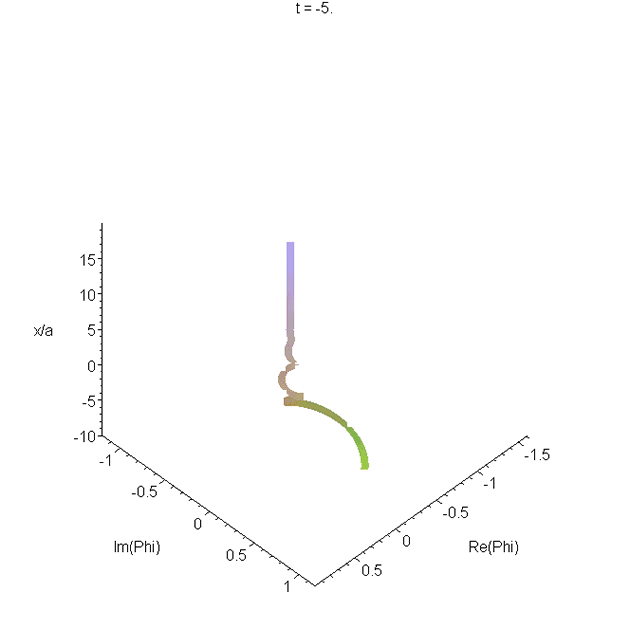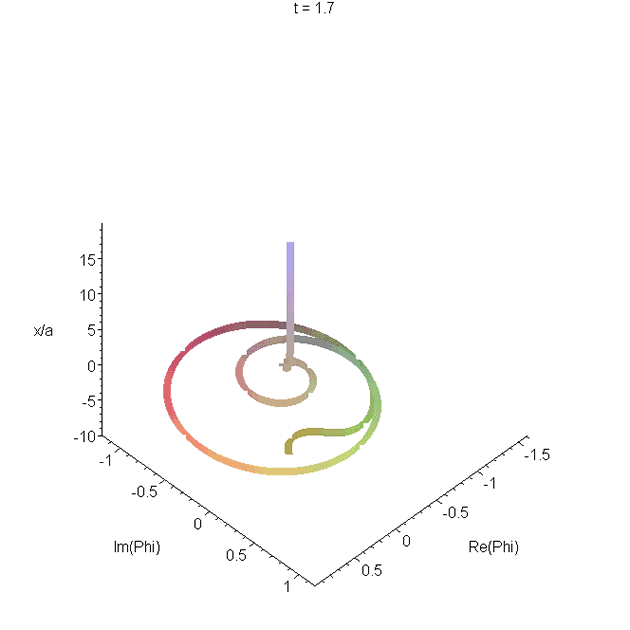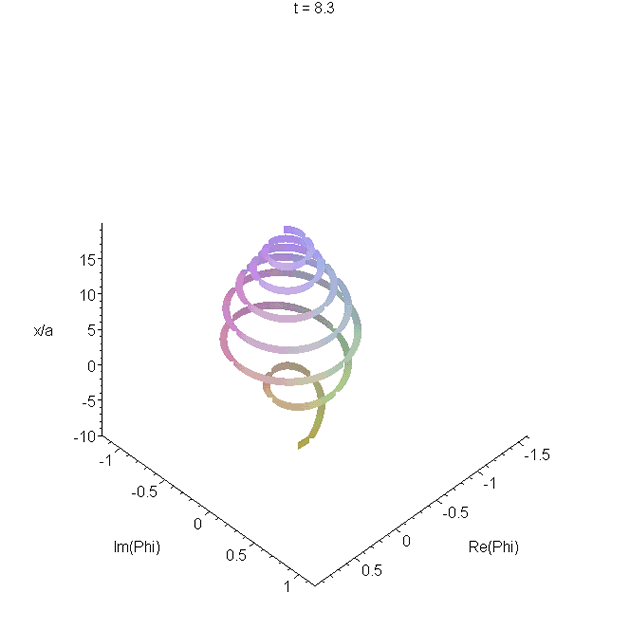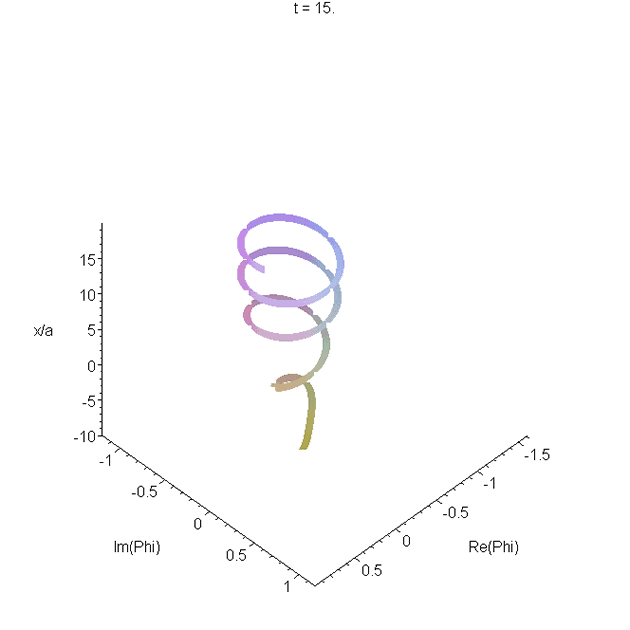
Motion of the wavepacket \(\Phi_1(x,t)\) through the potential region. The parameters used are as in A1. The real and imaginary parts of \(\Phi_1(x,t)\) are plotted as a function of \(x\), and animated. The resulting space curve changes helicity. Most of the curve is right-handed, but there is a left-handed region in the tail. The helicity is related to increase or decrease of the phase with \(x\). See problem 4 in Reflectionless eigenstates of the sech2 potential.
C1 Comparison of the motion of the wavepackets \(\Phi_0(x,t)\) and \(\Phi_1(x,t)\)
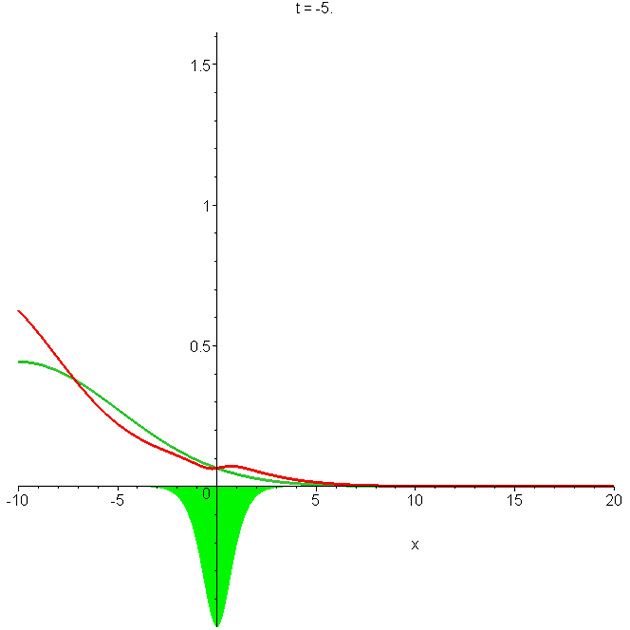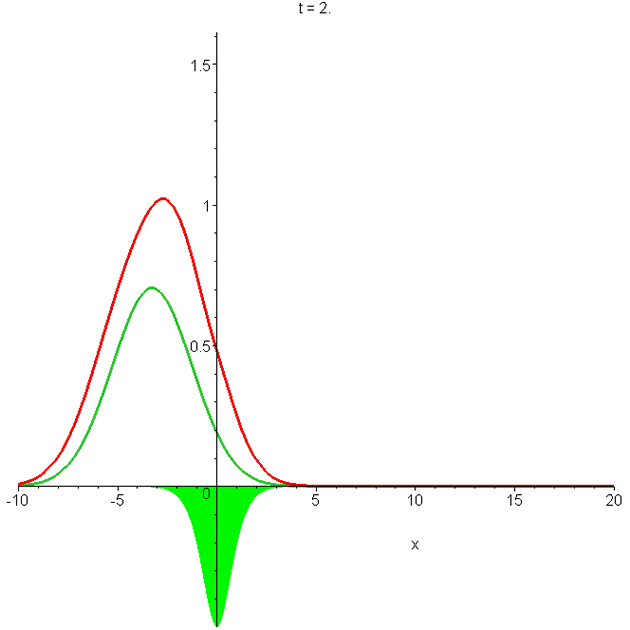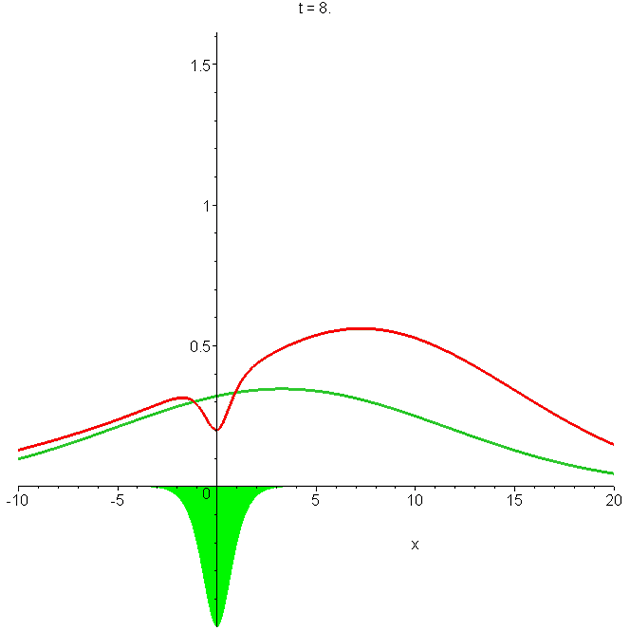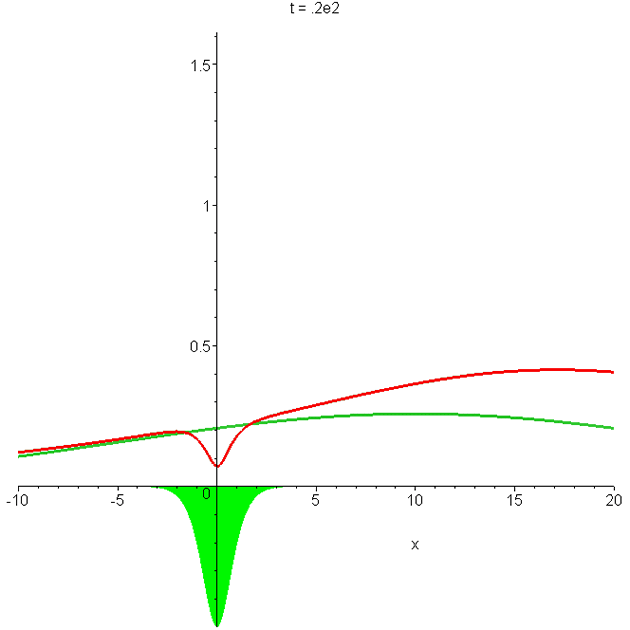
Animation of \(\left|{\Phi_0}\right|^2\) and of \(\left|{\Phi_1}\right|^2\). Parameters are as in A0 and A1. The larger packet is the sech2 solution. Note the indentation of the \(\left|{\Phi_1}\right|^2\) curve at the potential (shaded green), and the fact that it travels faster than the free-space packet (see Section IV of "Reflectionless eigenstates of the sech2 potential" ).
A2 Total reflection of a wavepacket by the potential \(\hbar/mx^2\)
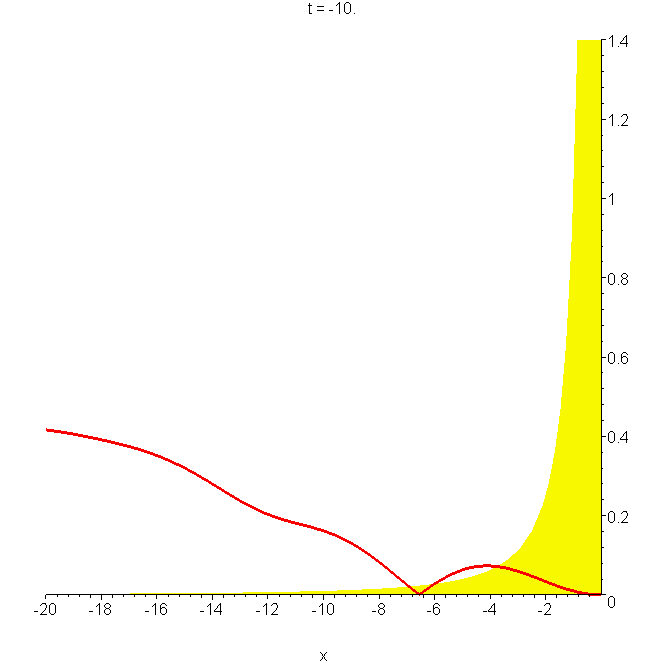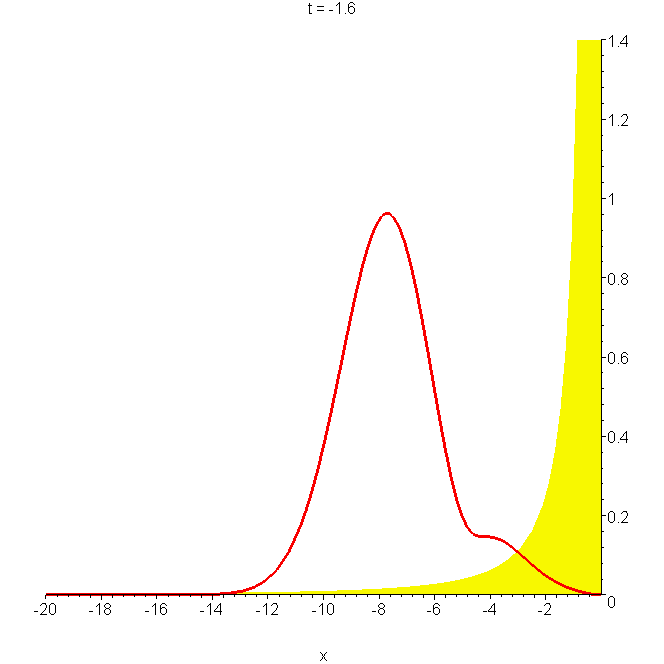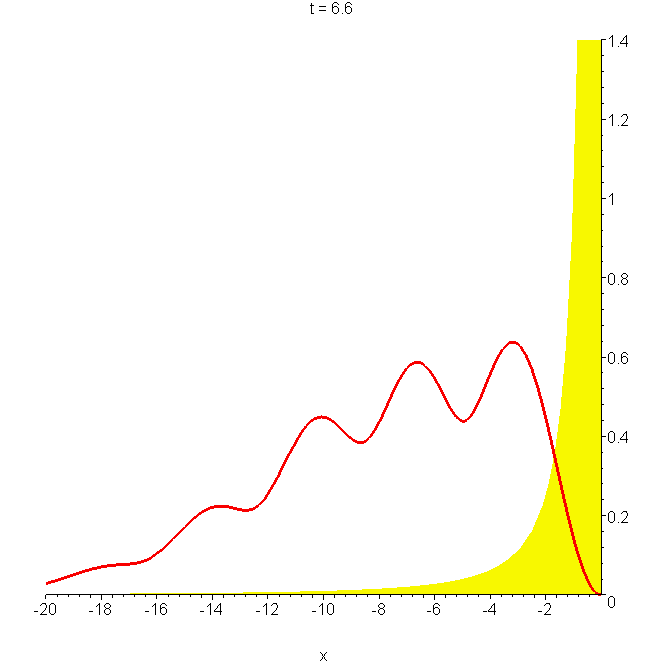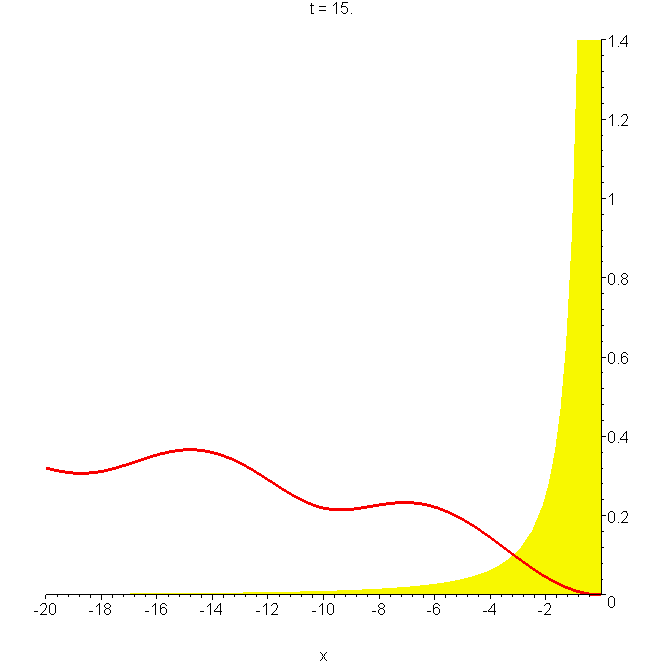
Total reflection of a wavepacket by the potential \(\hbar/mx^2\); the parameters are as in A0. Note the large probability \(\left|{\Phi}\right|^2\) near \(x=0\) at \(t\approx2.5b/v_0\), and the oscillations in the reflected part. The wavepacket is given by \begin{aligned} \Phi(x,t) & =\left(-\delta_x+\frac{1}{x}\right)[\Phi_0(x,t)-\Phi_0(-x,t)]\\ & =\left[\frac{1}{x}+\frac{x-x_0-ik_0b^2}{b^2+i\hbar{}t/m}\right]\Phi_0(x,t)-\left[\frac{1}{x}+\frac{x+x_0+ik_0b^2}{b^2+i\hbar{}t/m}\right]\phi_0(-x,t) \end{aligned} See "Reflection and non-reflection of particle wavepackets".
A3 Partial reflection of a wavepacket by the delta function repulsive potential \(V(x)=\frac{\hbar^2\kappa}{m}\delta(x)\)
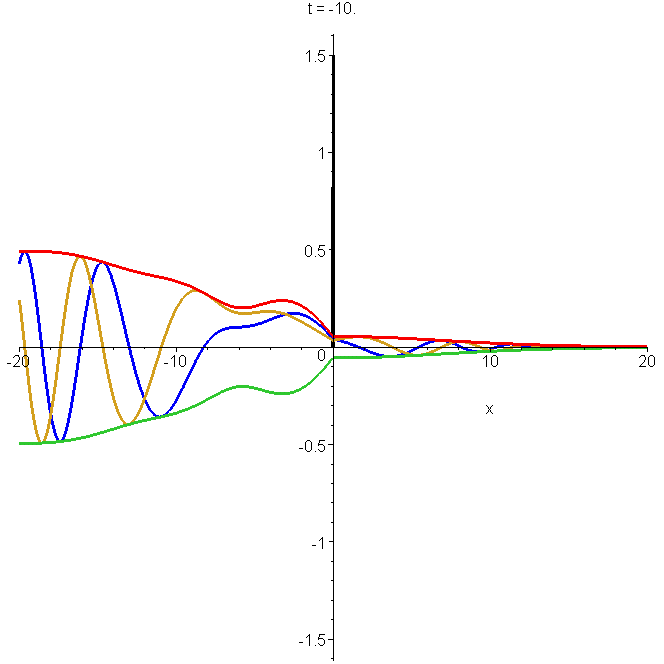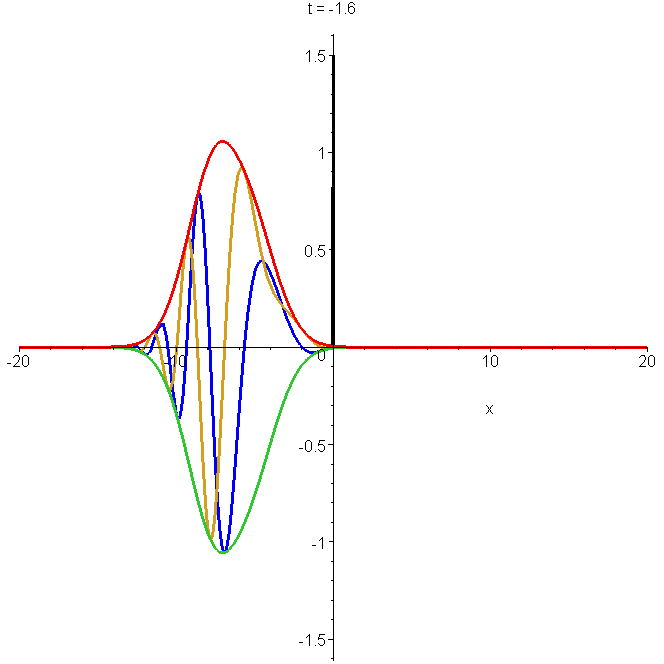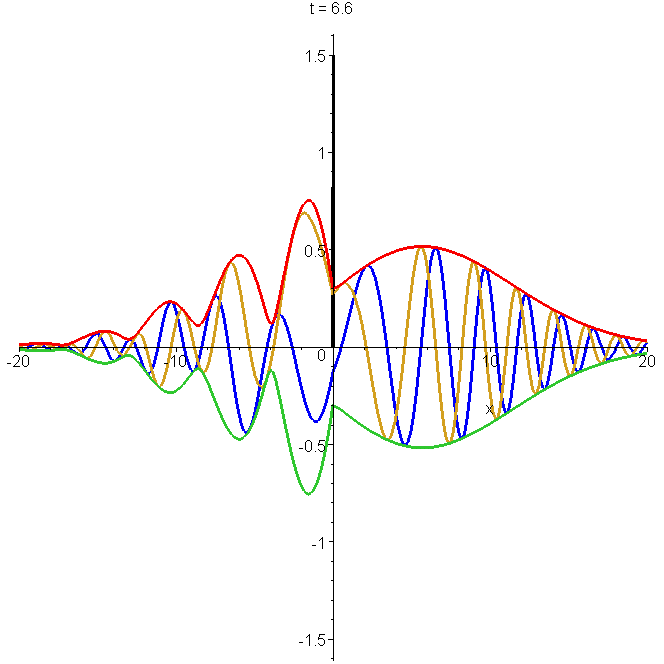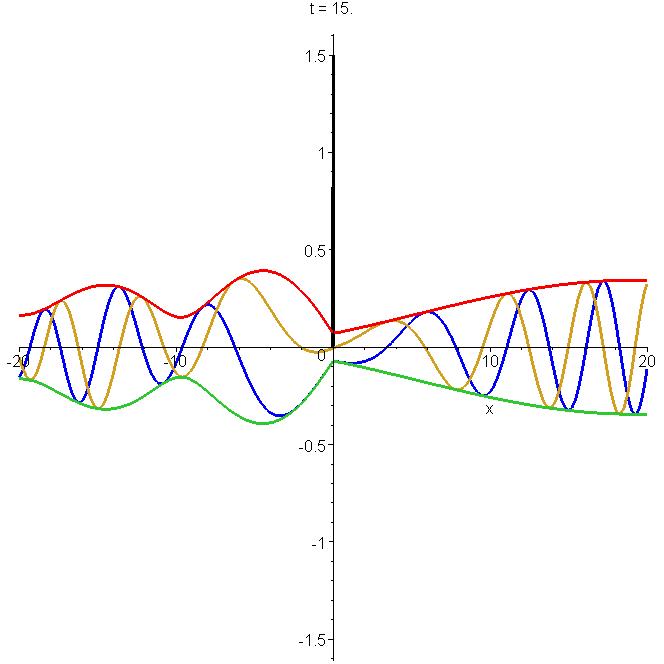
The plotted solution of Schrödinger's equation is \[\Phi(x,t)=\begin{cases} (-\delta_x+\kappa)\Phi_0(x,t)-\kappa\Phi_0(-x,t) & x \lt 0 \\ -\delta_x\Phi_0(x,t) & x \gt 0 \end{cases}\] where \(\Phi(x,t)\) is the free-space Gaussian wavepacket. The parameters are \(x_0=-5b\), \(k_0b=1\) and \(\kappa{}b=1\). Note the interference fringes in \(\left|{\Phi_0}\right|^2\) after reflection. The potential (at zero \(x\)) is indicated by a spike. See "Reflection and non-reflection of particle wavepackets".
A4 Contraction and spreading of the Airy wavepacket in its zero-momentum frame
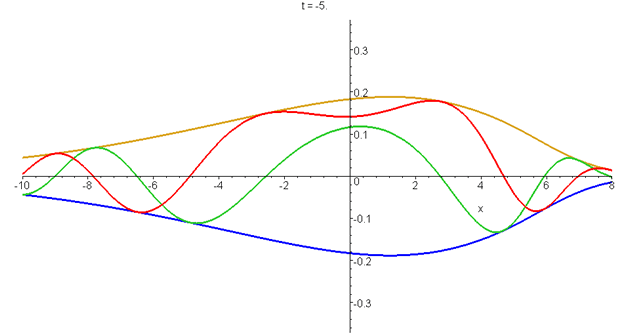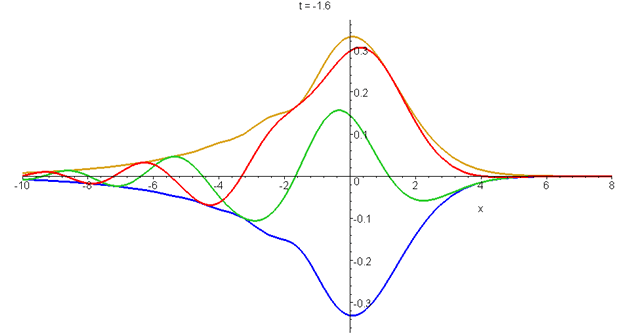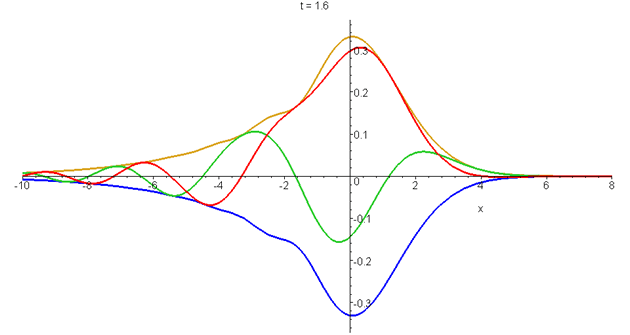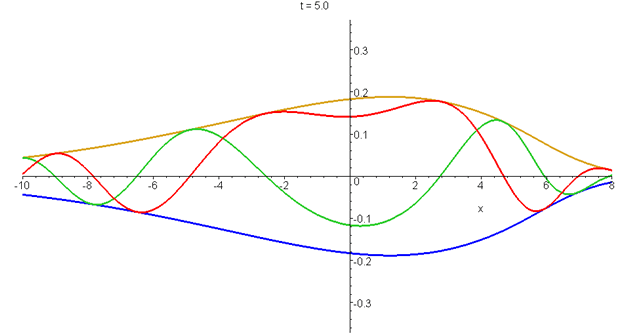
\[\psi(x,t)=Ai\left[q\left(x-ut+ivt-\frac{1}{2}at^2\right)\right]exp\left[i\frac{mat}{\hbar}\left(x-ut-\frac{1}{3}at^2\right)\right]exp\left[\frac{mv}{\hbar}\left(x+\frac{1}{2}v{}t-at^2\right)\right]\] in its zero-momentum (\(u=0\)) frame. The modulus and the real and imaginary parts of \(\psi\) are shown from \(t=-5\tau\) to \(t=d\tau\), where \(\tau=(\hbar/4ma^2)^{1/3}\). The unit of length is \(q^-1=(\hbar^2/2m^2a)^{1/3}\), and \(v\) is set equal to \((\hbar{a}/4m)^{1/3}\). The centre of probability remains fixed at \(q\langle{x}\rangle=-\frac{1}{4}\). See "Airy wavepacket solutions of the Schrödinger equation".
B4 Space curve of the Airy wavepacket in its zero-momentum frame
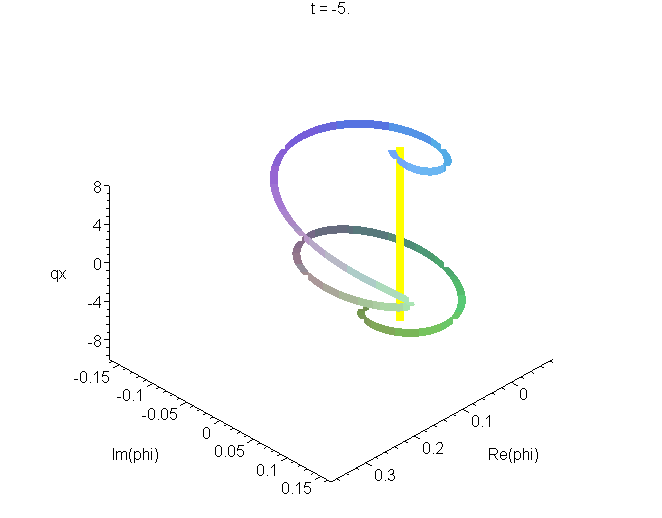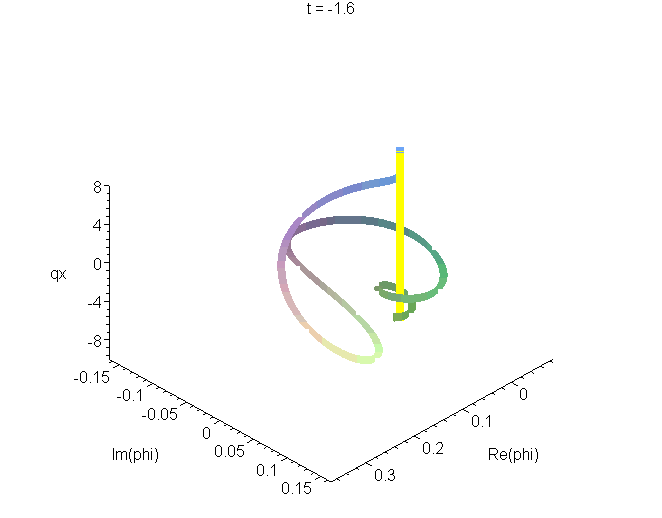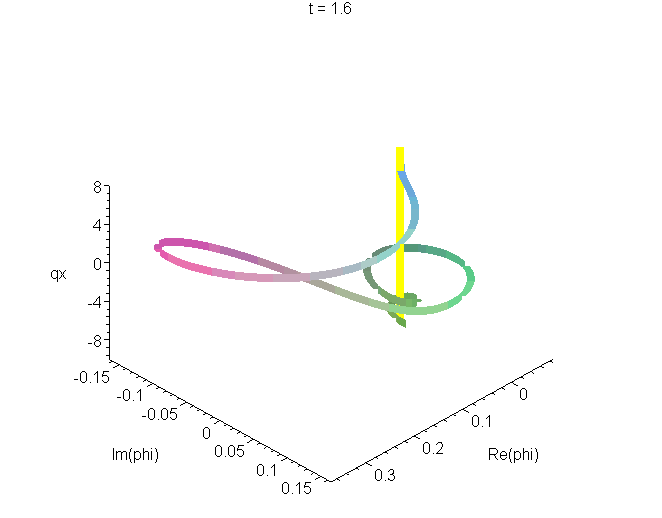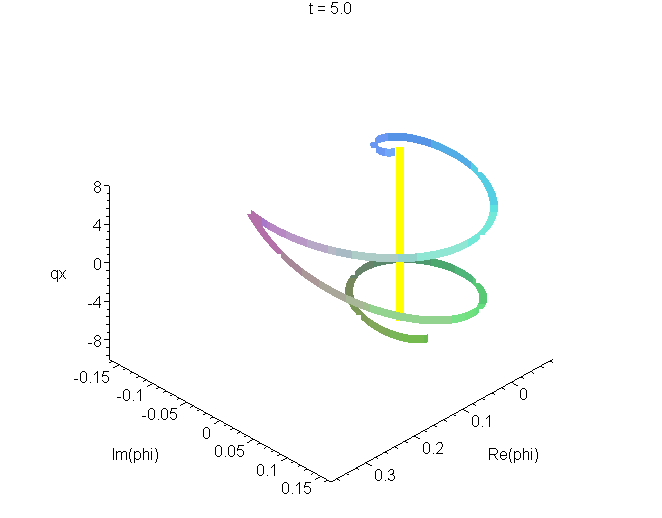
A space curve of the Airy packet \[\psi(x,t)=Ai\left[q\left(x-ut+ivt-\frac{1}{2}at^2\right)\right]exp\left[i\frac{mat}{\hbar}\left(x-ut-\frac{1}{3}at^2\right)\right]exp\left[\frac{mv}{\hbar}\left(x+\frac{1}{2}v{}t-at^2\right)\right]\] in its zero-momentum frame (\(u=0\)), from \(t=-5\tau\) to \(t=d\tau\), where \(\tau=(\hbar/4ma^2)^{1/3}\). The real and imaginary parts of \(\psi\) are plotted as the transverse coordinates, the vertical coordinate is \(qx\). The unit of length is \(q^-1=(\hbar^2/2m^2a)^{1/3}\), and \(v\) is set equal to \((\hbar{a}/4m)^{1/3}\), as in A4. See "Airy wavepacket solutions of the Schrödinger equation".
A5 Gaussian wavepacket in gravitational field
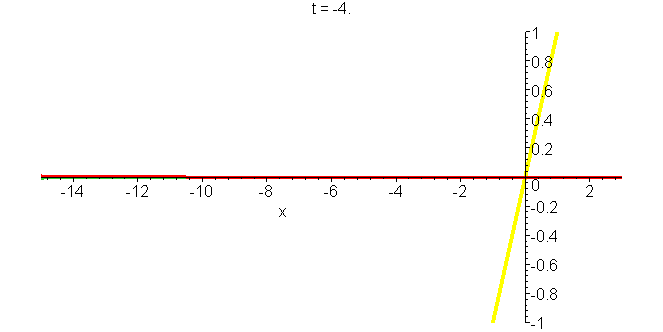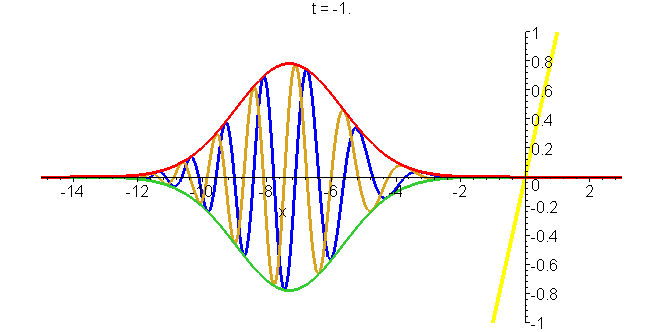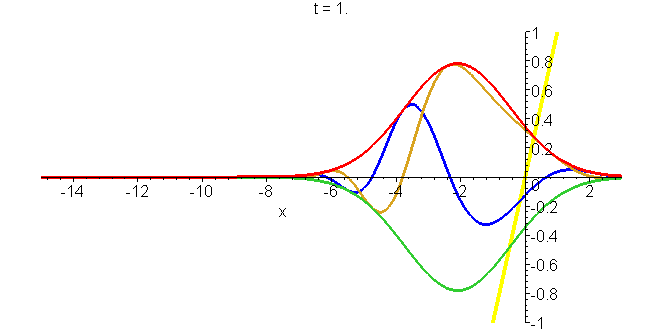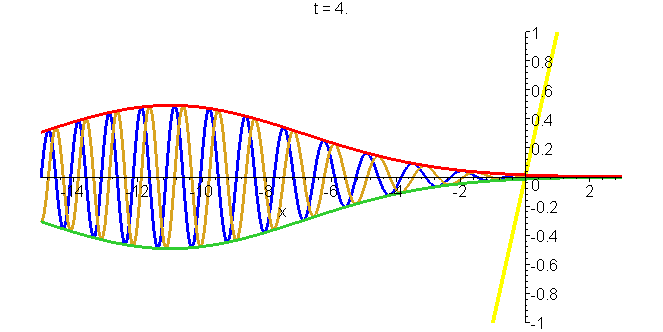
The rise and fall of a particle in the potential \(mgx\) (schematically indicated by the sloping line), as represented by an accelerated Gaussian packet \[\Phi(x,t)=\frac{b}{b^2+i\hbar{}t/m}exp\left[-\frac{imgt}{\hbar}\left(x+\frac{1}{6}gt^2\right)\right]exp\left[ik_0\left(x-x_0-\frac{1}{2}ut+\frac{1}{2}gt^2\right)-\frac{(x-x_0-ut+\frac{1}{2}gt^2)^2}{2(b^2+i\hbar{}t/m)}\right]\] The packet is tightest at time zero, spreading as time progresses (in either direction). The parameters are \(x_0=-3b\), \(k_0=2b^-1\), \(u=\hbar{}k_0/m=2\hbar/mb\), and \(g=2\hbar^2/m^2b^3\). Times are given in units of \(\tau=b/u=mb^2/2\hbar\). The real and imaginary parts of \(\phi\) can be seen in the animations, as well as the modulus (envelope of the real and imaginary parts). See "Construction of accelerating wavepackets".
A6 Schrödinger packet for a particle in a harmonic oscillator potential
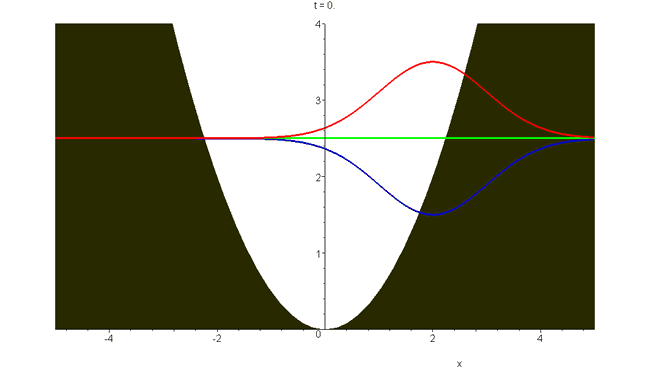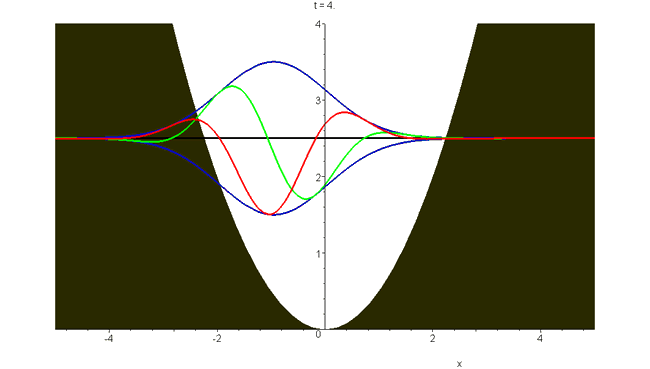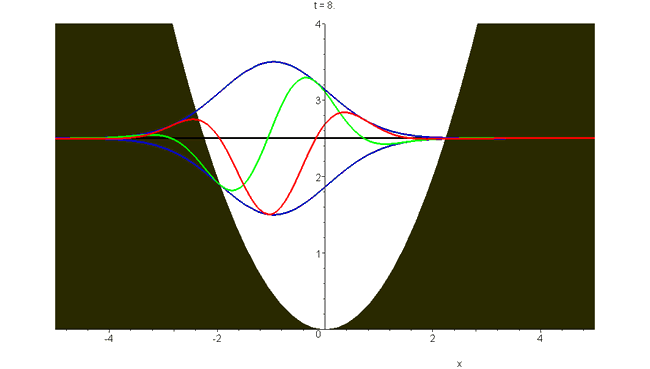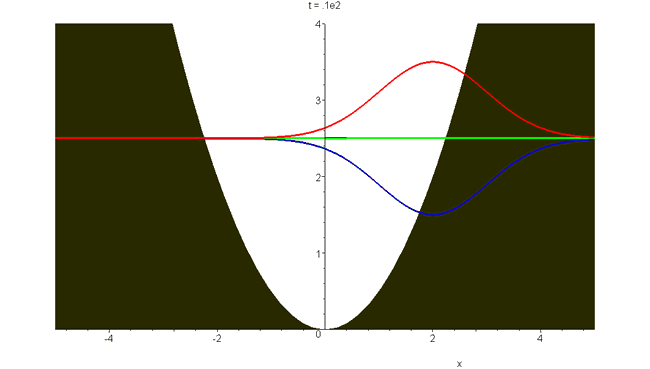
There are rather few closed-form solutions of Schrödinger's time-dependent equation for particles moving in a force field. The earliest (1926) is Schrödinger's harmonic oscillator wavepacket \[\Phi_S(x,t)=exp\left[-\frac{1}{2}(\xi-\xi_m\cos\omega{}t)^2-i\left(\frac{1}{2}\omega{}t+\xi\xi_m\sin\omega{}t-\frac{1}{2}\xi_m^2\sin\omega{}t\cos\omega{}t\right)\right]\] Here \(\xi=(m\omega/\hbar)^\frac{1}{2}x\), and the potential is \(V(x)=\frac{1}{2}m\omega^2x^2=\frac{1}{2}\hbar\omega\xi^2\). The absolute square is \(\left|{\Phi_S(x,t)}\right|^2=exp[-(\xi-\xi_m\cos\omega{}t)^2]\) and thus \(\Phi_S\) represents oscillatory motion within the oscillator well, at the classical frequency. This bound wavepacket does not contract or spread with time, in contrast to the unbound packets that have been shown in previous animations. The total energy is \(E=\frac{1}{2}\hbar\omega(1+\xi_m^2)\), and the animation shown has the dimensionless displacement \(\xi_m=2\). Real and imaginary parts (red and green), and plus and minus the modulus (blue), are plotted versus \(\xi\). See "Construction of accelerating wavepackets".
B6 Harmonic oscillator wavepacket: an animated space-curve
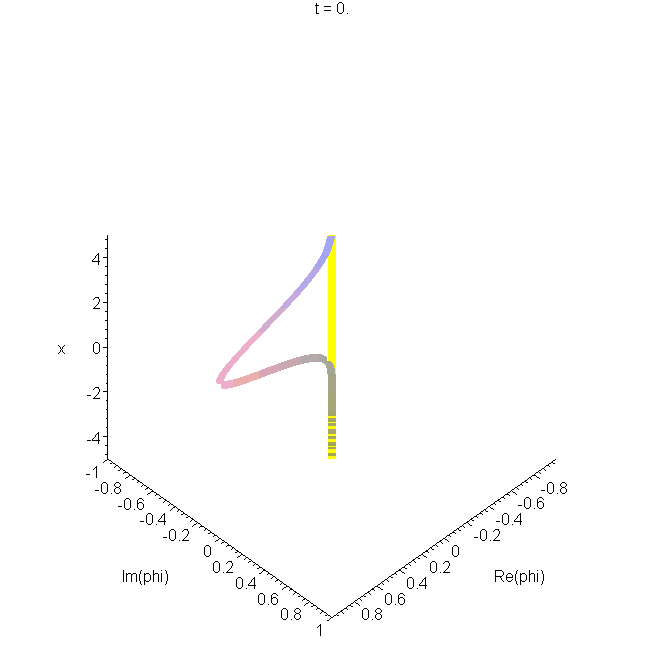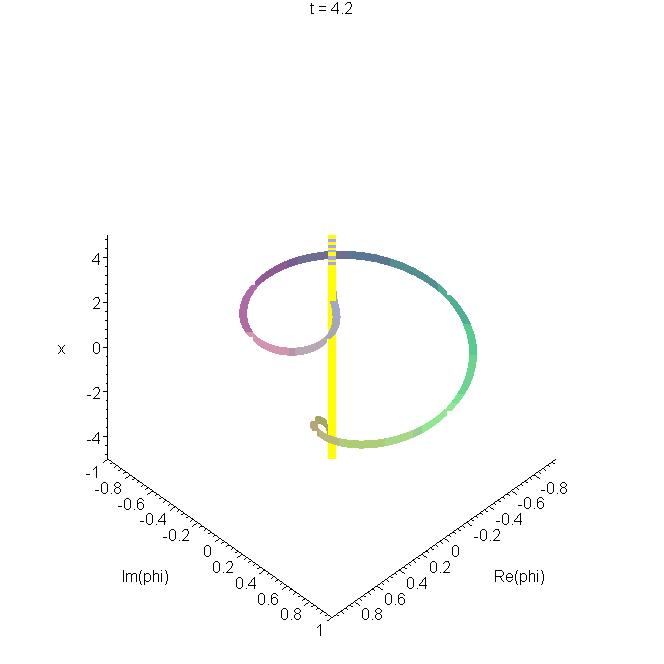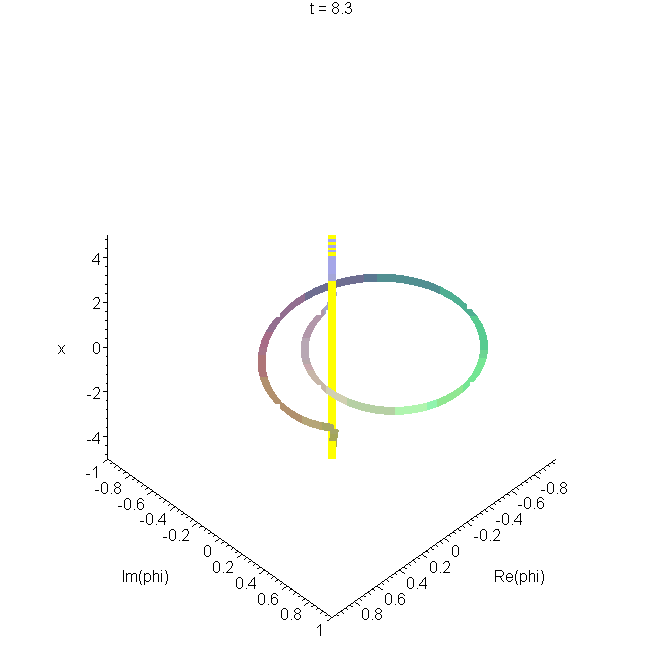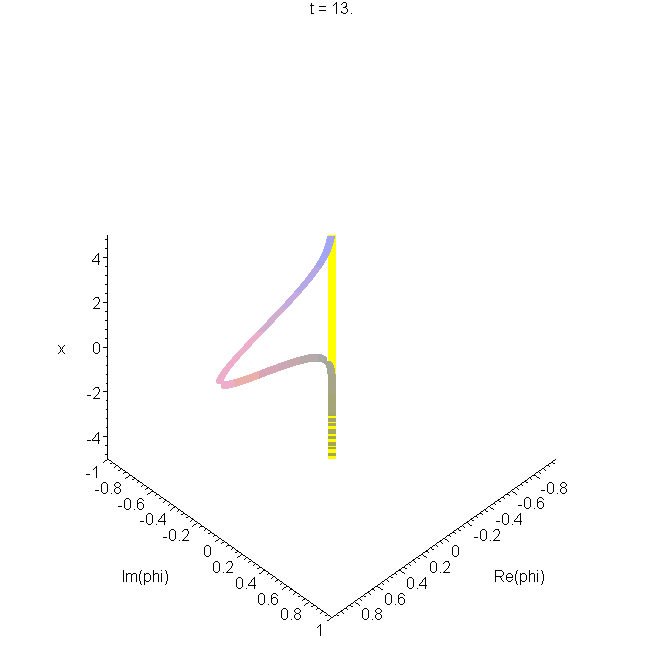
The real and imaginary parts of Schrödinger's harmonic oscillator wavepacket are plotted as a function of \(x\), and animated. This gives a space-curve developing in time, as we showed in the B0 and B1, for example. The space-curve represents the same information as is shown in A6, and the same parameters are used.
\(\Phi_S\) represents oscillatory motion within the oscillator well, at the classical frequency. The mathematical form is a precursor of the coherent states of quantum optics. See "Construction of accelerating wavepackets" .
C6 Packet based on first excited state of harmonic oscillator
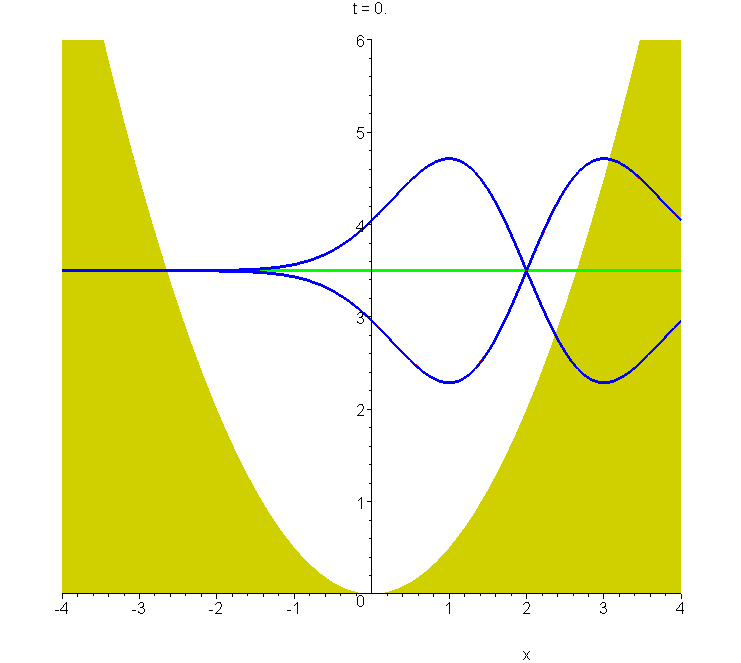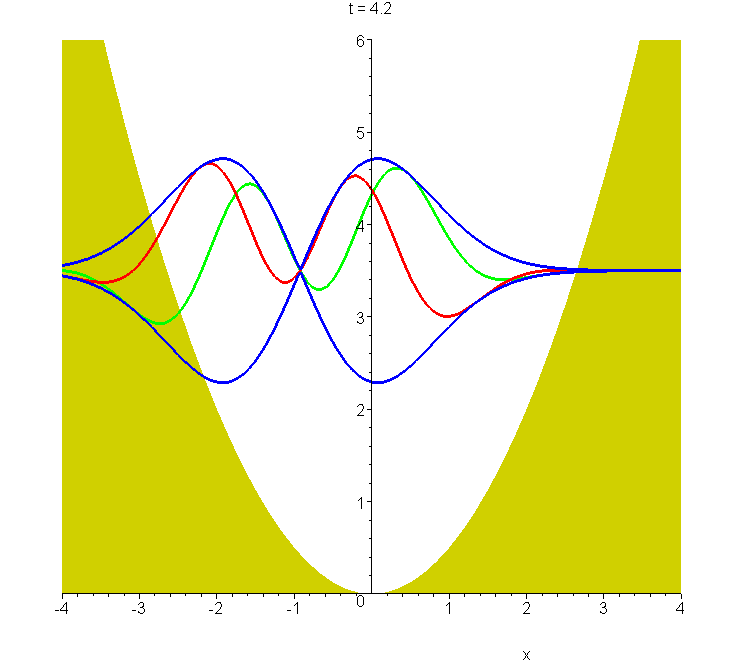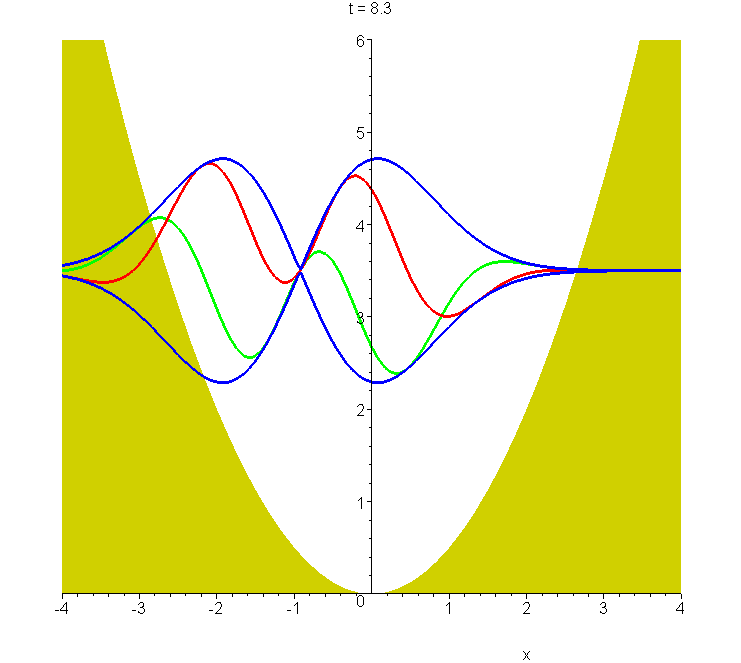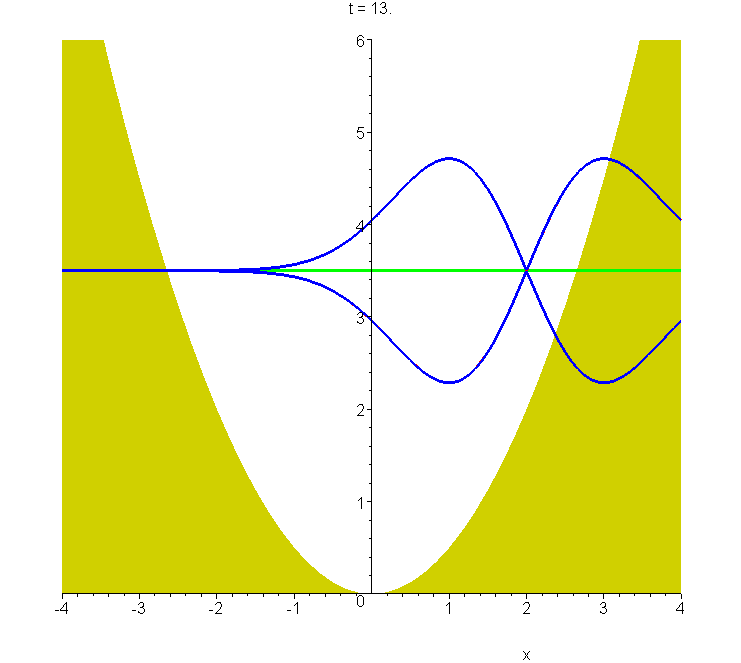
The oscillating wavepacket based on the first excited state of the harmonic oscillator, animated for \(\xi_m=2\) from \(t=0\) to \(t=2T\). The packet envelope keeps the same shape during the oscillation, as for the Schrödinger wavepacket, shown in A6. The harmonic potential is shown, in units of \(\hbar\omega\). The expectation value of the energy of the \(\xi_m=2\) packet is \(\frac{7}{2}\hbar\omega\), and the wavepacket modulus (blue) and real and imaginary parts (red and green) are drawn about this level. See "Construction of accelerating wavepackets".
A7 Quantum bouncer on a spring
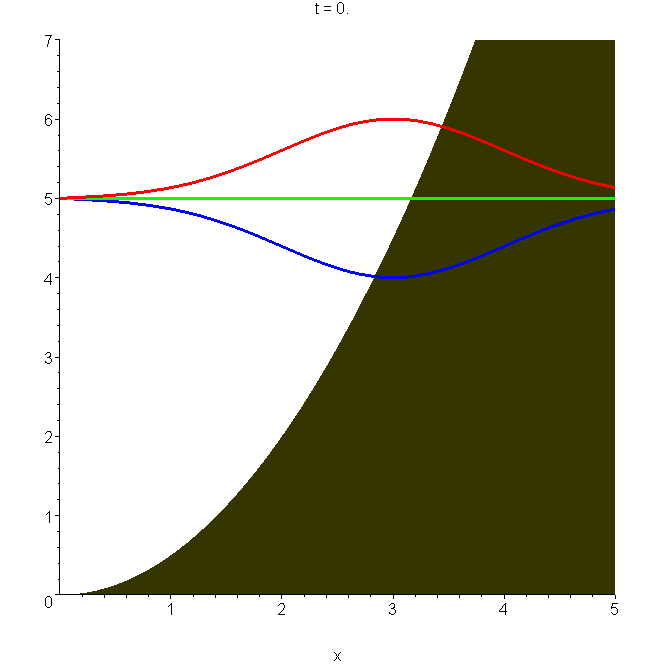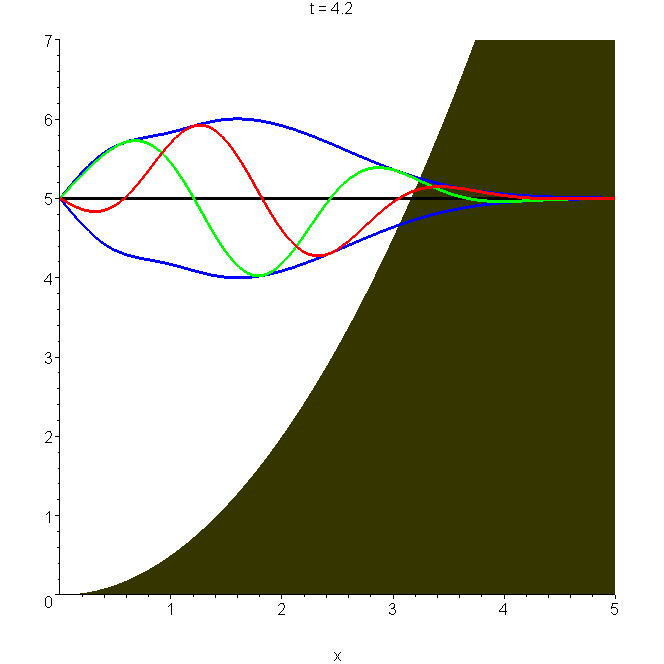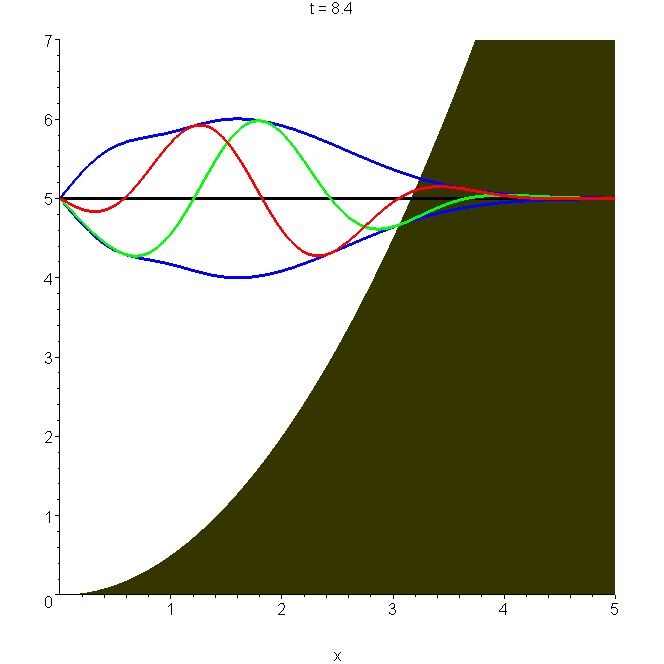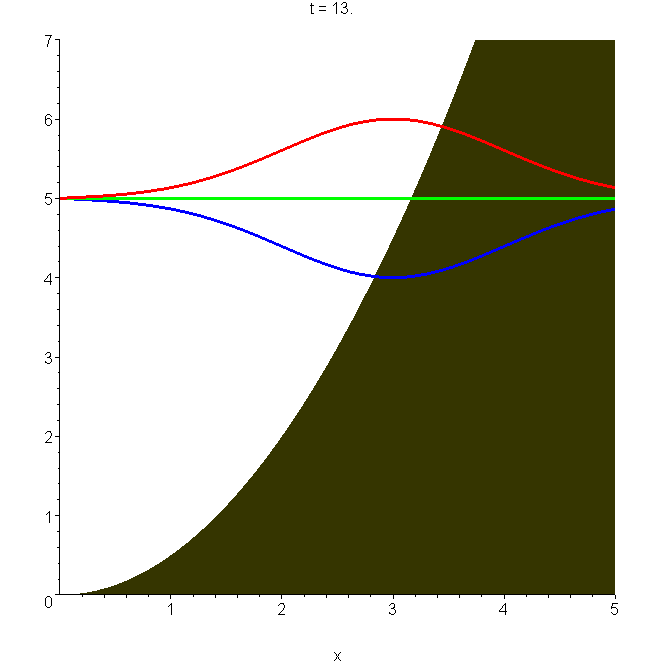
Imagine a quantum particle (an atom or a molecule, for example) attached to a hard wall by a spring (gravity is absent). An exact solution for the quantum motion is possible, in terms of Schrödinger's wavepacket (see A6 and B6): \(\Psi_S(x,t)=\Phi_S(x,t)-\Phi_S(-x,t)\). The animation shows the wavepacket oscillate through a full cycle, which takes time \(2T\), where \(T\) is the classical period of the harmonic oscillator without the reflecting wall. The classical period of the harmonic bouncer is \(T/2\), so it takes fully four classical oscillations to bring the wavepacket back to its original form! The dimensionless displacement \(\xi_m=(m\omega/\hbar)^\frac{1}{2}x_m\) in the animated packet has been set equal to 3. See "Quantum bouncer on a spring".
A8 Airy wavepacket in gravitational field
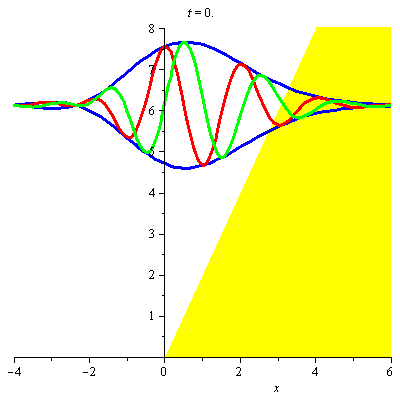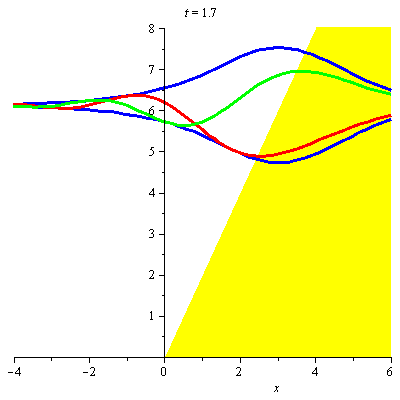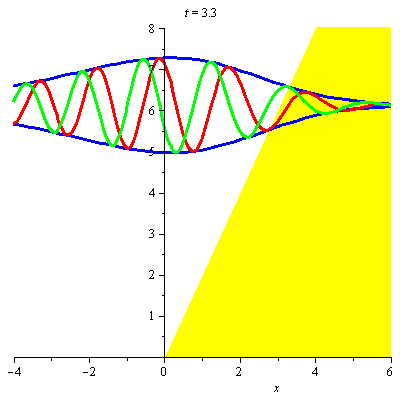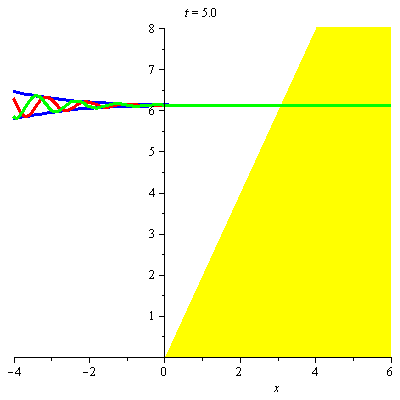
Airy wavepacket in a gravitational field, shown at times from \(t=0\) (its focal point), to \(t=5m/\hbar{q}^2\). The animation shows the modulus (blue) and the real and imaginary parts (red and green) of the wavepacket with parameters \(v=3\hbar{q}/m\), \(w=\hbar{q}/m\), \(g=4a\). These curves are raised to the corresponding value of \(\langle{E}\rangle\), namely \(\frac{49}{8}\hbar^2q^2/2m\). The classical turning point is at \(q\langle{x}\rangle=3\). The wavenumber \(q\) is given by \(q^3=2m^2a/\hbar^2\), and the numbers on the horizontal axis correspond to \(qx\). See "Construction of accelerating wavepackets".
